偏最小二乘回归方法（LS）背景介绍及研究焦点

偏最小二乘回归法(PLS) 背景介绍 在经济管理、教育、农业、社会科学、工程技术、医学和生物学等领域，多元线性回归分析是一种常用的统计分析和预测技术。 在多元线性回归中，一般采用最小二乘法（ Least ：OLS）来估计回归系数，使残差平方和最小，但当自变量之间存在多重相关时，最小二乘估计法往往失效。 然而，变量之间的多重相关问题在多元线性回归分析中危害很大，但却很普遍。 为了消除这种影响，常采用主成分分析（PCA），但主成分分析提取的主成分能更好地概括自变量系统中的信息，但带来了很多无用的噪声。 ，因此缺乏对因变量的解释力。 最小偏二乘回归法（n：PLS）就是应这种实际需要而产生和发展起来的一种具有广泛适用性的多元统计分析方法。 它首先由 S. 等人提出。 1983年成功应用于化学领域。 近十年来，偏最小二乘回归方法在理论、方法和应用方面都得到了迅速发展，并广泛应用于生物信息学、机器学习和文本分类等众多领域。 偏最小二乘回归法的主要研究重点是多因变量对多自变量的回归建模。 它与普通多元回归方法的主要区别在于它在回归建模过程中使用了信息综合和筛选技术。 .

不再是直接考虑因变量集和自变量集的回归建模，而是从变量系统中提取出几个对系统具有最佳解释力的新的综合变量（也称为成分），然后进行回归模仿他们。 偏最小二乘回归将建模型预测分析方法与非模型数据内容分析方法有机地结合起来，可以同时实现回归建模、数据结构简化（主成分分析）和两组变量之间的相关性时间。 分析（典型相关分析），它集成了多元线性回归分析、典型相关分析和主成分分析的基本功能。 下面简单介绍一下偏最小二乘回归的基本原理。 偏最小二乘法的工作目标 2.1 偏最小二乘法的工作目标 在一般的多元线性回归模型中，如果存在一组因变量Y={y，则可以很好地估计Y。它从这个公式很容易看出，由于(XX)一定是可逆矩阵，当X中的变量存在严重的多重相关时，或者当X中的样本点数相对于变量数明显偏少时，最少乘法估计会失败，会造成一系列的应用困难。 考虑到这个问题，提出了使用分量提取方法的偏最小二乘回归分析。 在主成分分析中，对于单个数据表X，为了找到最能概括原始数据的综合变量，提取第一主成分F1，使得F所包含的原始数据的变异信息可以达到最大值。 即在典型相关分析中，Var(F)max 提取 X 和 F)maxF1 之间的典型成分，以便从整体上研究两个数据表之间的相关性。 如果存在明显的相关性，则可以认为两个数据表之间也存在相关性。

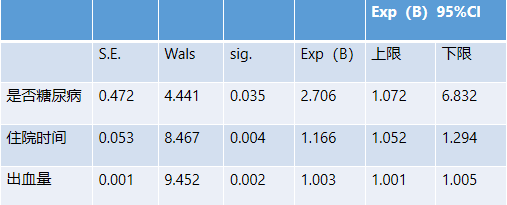
提取成分的做法在数据分析方法中很常见。 判别法中除了主成分和典型成分外，还有判别成分。 实际上，如果F是X数据表的某个分量，就意味着量的某种线性组合F=Xa偏最小二乘回归方法，而F作为一个综合变量，它所综合提取的信息将满足我们特殊的分析需要。 2.2 偏最小二乘回归分析的建模方法。 有 q 个因变量 {y}。 为了研究因变量和自变量之间的统计关系，观察n个样本点，从而形成自变量和因变量之间的关系。 数据表X=[x1,...，x和u1的相关度可以达到最大。 这两个要求表明 t 对因变量的分量 u 具有最强的解释力。 第一个分量 t 的回归和 Y 在 t1 上的回归。 如果方程达到令人满意的精度，则算法终止； 否则，将使用X被t解释后的残差信息和解释后的残差信息进行第二轮分量提取。 以此方式递归，直到可以达到满意的精度。 为了便于数学推导，首先将数据标准化。 X的标准化数据矩阵记为0P)n*p，Y的标准化数据矩阵记为F01，...，F0q的第一个分量，t1=E0w中的数据变化信息，根据原理成分分析 原则上应该有Var(t)(u)max 另一方面，由于回归建模的需要，也要求t和u1的相关性要达到最大值，即r(t1,u)max因此被积分，在偏最小二乘回归中，我们要求t和u1之间的协方差达到最大值，即Cov(t是求解下面的优化问题max

九软件 版权声明：以上发布的内容及图片均来源于网络，如有无意侵犯到您的权利，请联系我们及时删除！