加法和减法等算术运算在处理器逻辑设计中的应用
组合逻辑硬件建模设计(二)运算电路
加法和减法等算术运算在处理器逻辑设计中起着重要作用。 任何处理器的算术逻辑单元 (ALU) 都可以设计为执行加法、减法、递增和递减运算。 算法设计由 RTL 代码描述,以实现最佳区域和更少的关键路径。 本节介绍执行具有等效 RTL 描述的算术运算的重要逻辑块。
单位加法器 Adder
加法器用于执行两个二进制数的二进制加法。 用于有符号和无符号加法运算。
一位半加器
半加器有两个一位输入“a_in”、“b_in”,并生成两个一位输出“”、“”,其中“”是和或加法输出,“carry out”是进位。 表 2.9 是半加器的真值表,例 2.90 描述了 RTL。
表 2.9 半加器真值表
示例 2.9 半加器的可综合 RTL 代码
注:半加器作为加法的基本元件,全加器逻辑电路以半加器为例设计
图 2.9 合成后半加法器
综合后半加器如图 2.9 所示。 半加器的输入端口分别命名为“a_in”、“b_in”,输出为“”、“”
一位全加器
全加器用于对三个一位二进制输入执行加法运算。 一位二进制数称为“a_in”、“b_in”、“c_in”,一位二进制输出称为“”、“”。 表 2.10 是全加器的真值表,RTL 在例 2.10 中描述。
表 2.10 全加器真值表
示例 2.10 全加器的可综合代码。 注意:全加器占用面积较大,因此强烈建议使用多路复用器来实现加法器。 逻辑综合后的全加器如图2.10所示。 全加器的输入端口分别命名为'a_in'、'b_in'、'c_in',输出为''、''
图 2.10 综合后全加器
一位减法器
减法器用于执行两个二进制数的二进制减法。 本节介绍半减法器和全减法器。
一位半减法器
半减法器有两个一位输入“a”、“b”并产生两个一位输出“d”、“bor”。 其中“d”是减法器输出,“bor”是借位输出 ( )。 表 2.11 是半减法器的真值表,可综合 RTL 在示例 2.11 中进行了描述。
集成后半减法器如图 2.11 所示。 半加器的输入端口命名为“a”、“b”,输出端口命名为“d”、“bor”
表 2.11 半减器真值表
示例 2.11 半减法器的可综合代码。 注意:半减法器是用于执行二进制减法的基本组件。 全减法器逻辑电路的设计是使用半减法器作为一个组件来实例化的。
图 2.11 综合后半减法器
一位全减法器
全减法器用于执行三个一位二进制输入的减法。 一位输入数字被命名为“a”、“b”、“c”,一位二进制输出被命名为“d”、“bor.”。 表 2.12 是全减法器的真值表说明,RTL 在例 2.12 和图 2.12 中进行了描述。
表 2.12 全减法真值表
示例 2.12 全减法器的可综合代码。 注意:建议使用全加器进行减法,减法使用补码加法
图 2.12 综合后全减器
集成的全减法器如图 2.12 所示。 全减法器的输入端口命名为“a”、“b”、“c”,输出端口命名为“d”、“bor”
多位加法器和减法器 Multi-bit and
多位加法器和减法器用于处理器算术单元的设计。 逻辑密度取决于加法器或减法器的输入位数。
四路全加器
许多实际设计使用多位加法器和减法器。 使用基元作为全加器来执行加法是业界实践证明的最佳方式。 例如,如果设计人员需要实现四位加法器的设计逻辑,则需要四个全加器。 对两个四位二进制数“A”、“B”进行加法运算,如例 2.13 所示。 最后的结果是四位加法,在“S”处输出。 进位是Ci,出位是Co。
集成的四位加法器如图 2.13 所示。 四位加法器的输入端口分别命名为“A”、“B”和“Ci”,输出端口分别命名为“S”和“Co”。
示例 2.13 四位加法器的可综合代码。 注:四位加法运算使用四个全加器。根据有符号或无符号加法需求,可以修改代码
图 2.13 综合后的四位加法器
四位加法器和减法器
加法和减法都设计为使用加法器来完成。 可以使用二进制补码加法执行减法。 例如表2.13所示的场景。
集成的四位加法器/减法器如图 2.14 所示。 示例 2.14 中的四位加法器/减法器的输入端口命名为“A”、“B”和“Ci”,输出端口命名为“S”。 “公司。” 当控制输入 SUB 等于逻辑“0”时,它将执行加法,而当控制输入 SUB 等于逻辑“1”时,它将执行减法,即 2 的补码加法。
表 2.13 加减法运算表
示例 2.14 四位加法器和减法器的可综合代码。 请注意,考虑到子控制,输入 Ci 和 S4 在综合逻辑中充当 CO。 在这里,使用的资源是一个二进制全加器来执行加法和减法。 减法运算仅使用加法器执行。资源共享和资源利用将在后面讨论
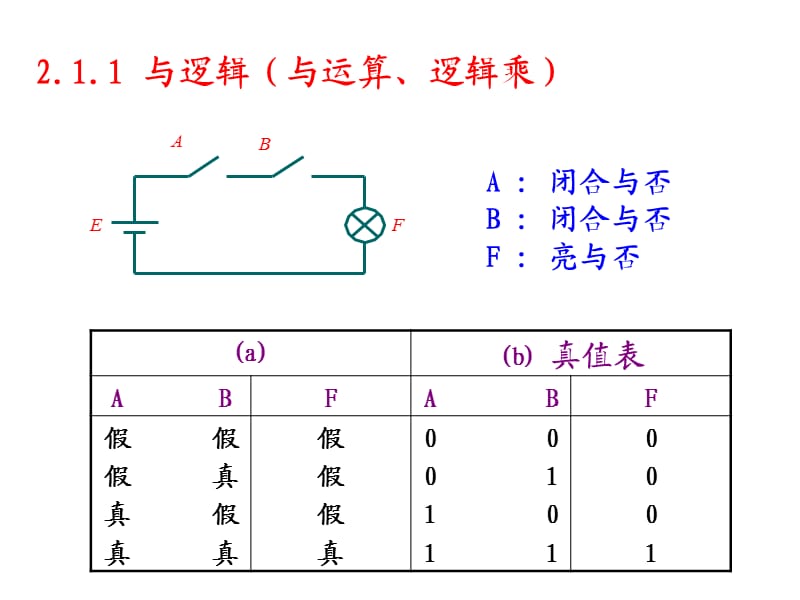
图 2.14 合成后的四位加法器/减法器
比较器和奇偶校验检测器
在大多数实际场景中:比较器用于比较两个二进制数是否相等。 奇偶校验器用于计算给定二进制数的奇偶校验。 对于设计工程师来说,更好地理解这一点变得非常重要。
二进制比较器
二进制比较器用于比较两个二进制数。 如前所述,支持四值逻辑,即逻辑“0”、逻辑“1”、未知“x”和高阻抗“z”。 支持逻辑相等运算符(==)和不等运算符(!=),用于描述两个数字的比较。 这些运算符都是可综合的。
表 2.14 比较运算表
例如,如表所示; 当A和B相等时,输出“Y”赋给“A”和“B”异或,不相等时,输出“Y”赋给“A”,“B”与运算"(示例 2.15)。
综合后的等效表示如图 2.15(例 2.15)所示。
示例 2.15 一位比较器的可综合代码。 注意:对于任何操作数“x”或“z”,可综合 RTL 代码中使用的逻辑相等和不等运算符与 false 比较
图 2.15 合成后的等效比较器
奇偶检测器
奇偶校验检测器用于检测二进制数字串的奇偶校验。 对于偶数个 1,输出为逻辑“0”,对于奇数个 1,输出为逻辑“1”四位加法器逻辑图,则 RTL 可以如例 2.16 所示描述。
示例 2.16 奇偶检测器的可合成代码。注意:奇偶检测器主要用作 DSP 应用程序和加密引擎的集成模块
表 2.15 奇偶检测器操作表
| 条件 | 说明 | | :-------- | :--: | | 奇校验 1| 将输出分配为逻辑 1| | 偶校验 1| 将输出分配为逻辑 0|
图 2.16 综合后奇偶检测器
奇偶检测器的操作表如下表2.15所示。 奇数个 1 的输出为逻辑“1”,偶数个 1 的输出为逻辑“0”。 集成表示如图 2.16 所示。
转码器
本节介绍设计中常用的转码器。 顾名思义,代码转换器用于将代码从一种数字系统转换为另一种数字系统。 在实际场景中,可用于二进制到格雷码(to gray)和格雷码到二进制的转换器(gray to)。
二进制到格雷码转换器
二进制数系统的基数是2,对于任何多位二进制数,不稳定的变化可能一次是一位或多位。 但是在格雷码中,一次只改变一位。
例 2.17 中描述了四位二进制到格雷码转换的 RTL 描述。
示例 2.17 用于四位二进制到格雷码转换器的可合成代码。注:格雷码用于多时钟域设计,以将控制信息从一个时钟域传输到另一个时钟域
图 2.17 合成后的四位二进制灰度转换器
集成表示如图 2.17 所示。
格雷码到二进制码转换器
格雷码转换器与 -to-Gray 的 RTL 描述相反,即例 2.18 中描述的四位格雷码转换。 集成表示如图 2.18 所示。
示例 2.18 四位格雷码到二进制码转换器的可合成代码。注:格雷码用于格雷码计数器实现,也常用于纠错机制
图 2.18 合成后的四位格雷码转二进制
定期总结
如前面提到的; 以下是实现组合逻辑 RTL 时需要考虑的要点。
通过共享算术资源最小化区域使用。
使用灵敏度列表中的所有所需信号以避免仿真和合成不匹配。
避免三态逻辑并使用具有适当使能电路的多路复用器来实现所需的逻辑。
支持四值逻辑,分别为逻辑'0'、逻辑'1'、未知'x'、高阻抗'z'
减少设计中加法器的使用。 加法器可以使用多路复用器来实现。
NAND 和 NOR 是通用逻辑门,可用于实现任何组合或时序逻辑。
数字硬件建模——换个角度理解(二)
组合逻辑硬件建模与设计(一)逻辑门
数字硬件建模——换个角度理解(一)
想用FPGA加速神经网络,必须了解这两个开源项目
数字硬件建模综述
九软件 版权声明:以上发布的内容及图片均来源于网络,如有无意侵犯到您的权利,请联系我们及时删除!